0%

数独与回溯法

发表于 更新于 分类于
本文字数： 3k 阅读时长 ≈ 4 分钟

数独是一种数学逻辑游戏，游戏由9×9个格子组成，玩家需要根据格子提供的数字推理出其他格子的数字。游戏设计者会提供最少17个数字使得解答谜题只有一个答案。

数独的解法需 遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 -w285

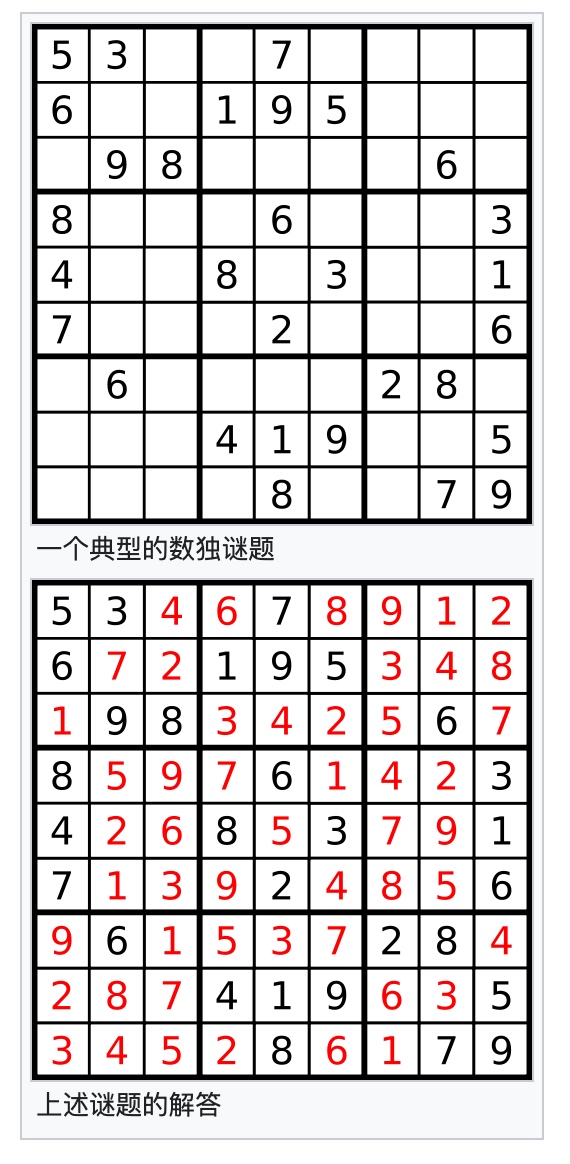
虽然玩法简单，但提供的数字却千变万化，所以很适合用程序来求解。

类似这种需要穷举的问题一般采用回溯法，也就是暴力求解，在最坏的情况下时间复杂度为指数。

回溯法

回溯法采用试错的思想，它尝试分步的去解决一个问题。在解决问题的过程中，如果现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。

回溯法通常用最简单的递归方法来实现，下面是回溯法的一般结构。
理解回溯法首先要理解递归，理解递归的过程，以及递归的返回值。可以通过查看斐波那契数列的递归实现的调用栈来理解递归的过程。

1
2
3
4
5
6
7
8
9
10
11
def backtracking(args):
    if can_stop(args):  # 判断是否终止，限制了递归深度
        if need():   # 必要时收集递归子树的叶子节点的结果
            collect_result()
        return

    for choice in get_all_choices(args):  # 针对每一种情况, 情况的个数也就是每一层的广度
        set_state(args, choice)  # 暂时选择该项
        process(args)   # 该节点数据加工
        backtracking(args)   # 递归进入下一层次
        revert_state(args, choice)   # 撤销当前选择

暴力解法

回到数独解法上来

首先看最简单的暴力解法

这里有几个点和模板不一样

  • 由于把整个棋盘都填满游戏就终止了，所以不需要can_stop判断
  • 每层递归会填满一个空位，递归的最大深度就是空位的个数。
  • 数独棋盘都填满才算一个解，所以每层递归get_all_choices最多有 行 x 列 x 数字取值 = 9 x 9 x 9 种情况
  • 由于数独规则的约束，行、列、九宫格内数字不能重复，所以天然有部分剪枝
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 0 代表空位
board = [
    [0, 8, 6, 9, 0, 2, 0, 0, 0],
    [0, 0, 7, 0, 0, 0, 0, 0, 0],
    [5, 2, 0, 0, 0, 7, 0, 0, 0],
    [2, 0, 0, 0, 0, 0, 0, 0, 6],
    [0, 0, 5, 0, 0, 0, 0, 0, 0],
    [0, 3, 1, 0, 0, 6, 0, 8, 2],
    [0, 0, 0, 4, 0, 9, 6, 5, 0],
    [0, 0, 0, 0, 1, 0, 2, 0, 3],
    [4, 1, 0, 6, 0, 5, 0, 0, 0],
]

EMPTY = 0
def sodoku(board):
    def can_put(board, row, col, c):
        for i in range(9):
            if board[i][col] != EMPTY and board[i][col] == c:  # 行不冲突
                return False
            if board[row][i] != EMPTY and board[row][i] == c:  # 列不冲突
                return False
            x, y = row // 3 * 3 + i // 3,  col // 3 * 3 + i % 3
            if board[x][y] != EMPTY and board[x][y] == c:  # 九宫不冲突
                return False
        return True

    def solve(board):
        for i in range(9):
            for j in range(9):
                if board[i][j] == EMPTY:
                    for c in range(1, 10):
                        if can_put(board, i, j, c):
                            board[i][j] = c
                            if solve(board):
                                return True
                            else:
                                board[i][j] = EMPTY
                    return False
        return True
    return solve(board)

剪枝

所谓的剪枝，就是递归每一层的时候，并不是所有情况都是有效的，可以跳过这些分支。

-w351

以该题为例，第一行第三列可选取值并不是1到9，而是1，2，4，而且随着我们不断把空位填满，越后面的点选择越少。
可以用集合存储每个空位的行、列、九宫方向的可选值，三者交集就是该点的可选值。（用位替换集合还可以进一步优化算法）
因为填充一个空位，会影响该位置行、列、九宫上的所有空位的取值，所有不直接存储该点的可选值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
EMPTY = 0
def sodoku(board):
    def solve(board):
        for i in range(9):
            for j in range(9):
                box_index = (i // 3 ) * 3 + j // 3
                if board[i][j] == EMPTY:
                    for c in (rows[i] & columns[j] & boxes[box_index]):    # 通过集合来剪枝
                        # 设置状态
                        board[i][j] = c
                        tmp = [False, False, False]
                        for idx, elem in enumerate((rows[i], columns[j], boxes[box_index])):
                            if c in elem:
                                elem.remove(c)
                                tmp[idx] = True
                        # 进入下一层递归
                        if solve(board):
                            return True
                        # 还原状态
                        board[i][j] = EMPTY
                        for idx, elem in zip(tmp, (rows[i], columns[j], boxes[box_index])):
                            if idx:
                                elem.add(c)
                    return False
        return True

    # 验证题目是否合法, 初始化每一格可选择项
    rows = [set(range(1,10)) for i in range(9)]  # 行内所有点的可选值
    columns = [set(range(1,10)) for i in range(9)]  # 列
    boxes = [set(range(1,10)) for i in range(9)]  # 九宫
    for i in range(9):
        for j in range(9):
            num = board[i][j]
            if num != EMPTY:
                num = int(num)
                box_index = (i // 3 ) * 3 + j // 3
                if num not in rows[i]:
                    return False
                rows[i].remove(num)
                if num not in columns[j]:
                    return False
                columns[j].remove(num)
                if num not in boxes[box_index]:
                    return False
                boxes[box_index].remove(num)
    return solve(board)

参考

https://zh.wikipedia.org/wiki/%E6%95%B8%E7%8D%A8
https://zh.wikipedia.org/wiki/%E5%9B%9E%E6%BA%AF%E6%B3%95
https://www.jianshu.com/p/8e694d079a76