0%

IEEE 754 与浮点数的二进制表示

发表于 更新于 分类于
本文字数： 2.3k 阅读时长 ≈ 3 分钟

在计算机科学中，浮点（英语：floating point，缩写为FP）是一种对于实数的近似值数值表现法, 类似于十进制的科学计数法.

科学记数法

在科学记数法中，一个数被写成一个”实数”与一个10的n次幂的积

其中：

  • $n$ 必须是一个整数, 可称之为指数。
  • $a$ 必须是[1, 10)区间内的实数，可称为有效数或尾数。

类似的，二进制的科学计数法则是 $\pm a \times 2 ^ n$ ，不同的是 $a$ 必须是[1, 2)区间内的实数。

所以浮点数的二进制表示，就是用二进制位表示为 $\pm a \times 2 ^ n$ 。

IEEE 754浮点数表示

所以，我们可以将一定长度的二进制位分成三个部分，用来分别表示 $\pm$、$n$、$a$ ，而IEEE 754就是具体实现的标准。

IEEE二进制浮点数算术标准（IEEE 754）是20世纪80年代以来最广泛使用的浮点数运算标准，为许多CPU与浮点运算器所采用。

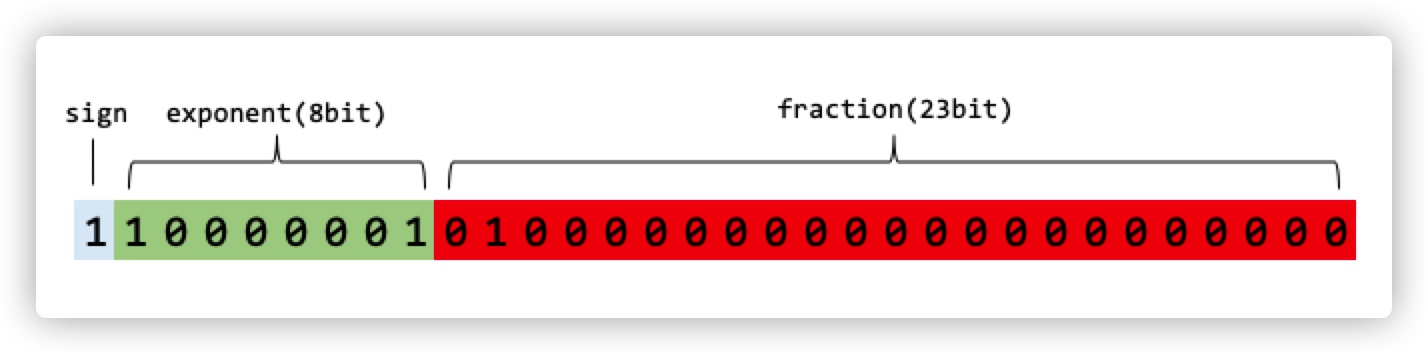
IEEE 754规定，对于32位的浮点数，最高的1位表示符号 $\pm$ 记为s(sign)，接着的8位表示指数 $n$ 记为E(exponent)，剩下的23位为有效数 $a$ 记为M(fraction)。

8位二进制位，能表示的256个数值，由于指数有正有负，标准规定从-127开始计数，也就是-127到128（与有符号数的实现不同），而且-127和128被用作特殊值处理，见下方特殊值。

同时，由于M的整数部分永远是1，我们可以只表示其小数部分，记为N。

也就是最终可表示为 $s \times 2 ^ E \times (1+N)$ 。

具体各部分拆解如下，其中 $a0$ 到 $a{31}$ 对应32个二进制位的值，为0或者1。

以十进制的 $-5.0$ 为例，可表示为 $-1.25 \times 2 ^ 2$。那么，s=1，N=0.25，E=2。
具体来说

特殊值

这里有三个特殊值需要指出：

  • 如果指数是0并且尾数的小数部分是0，这个数±0（和符号位相关）
  • 如果指数的二进制位全为1并且尾数的小数部分是0，这个数是±∞（同样和符号位相关）
  • 如果指数的二进制位全为1并且尾数的小数部分非0，这个数表示为非数（NaN）。

单精度浮点数各种极值情况：

类别 正负号 实际指数 有偏移指数 指数域 尾数域 数值
零 0 -127 0 0000 0000 000 0000 0000 0000 0000 0000 0.0
负零 1 -127 0 0000 0000 000 0000 0000 0000 0000 0000 −0.0
1 0 0 127 0111 1111 000 0000 0000 0000 0000 0000 1.0
-1 1 0 127 0111 1111 000 0000 0000 0000 0000 0000 −1.0
最小的非规约数 * -126 0 0000 0000 000 0000 0000 0000 0000 0001 ±2−23 × 2−126 = ±2−149 ≈ ±1.4×10-45
中间大小的非规约数 * -126 0 0000 0000 100 0000 0000 0000 0000 0000 ±2−1 × 2−126 = ±2−127 ≈ ±5.88×10-39
最大的非规约数 * -126 0 0000 0000 111 1111 1111 1111 1111 1111 ±(1−2−23) × 2−126 ≈ ±1.18×10-38
最小的规约数 * -126 1 0000 0001 000 0000 0000 0000 0000 0000 ±2−126 ≈ ±1.18×10-38
最大的规约数 * 127 254 1111 1110 111 1111 1111 1111 1111 1111 ±(2−2−23) × 2127 ≈ ±3.4×1038
正无穷 0 128 255 1111 1111 000 0000 0000 0000 0000 0000 +∞
负无穷 1 128 255 1111 1111 000 0000 0000 0000 0000 0000 −∞
NaN * 128 255 1111 1111 non zero NaN
* 符号位可以为0或1 .

浮点数与二进制字符串转换

1
2
3
4
5
6
7
8
9
10
11
def binary_to_float(data):
    assert len(data) == 32
    sign = (-1) ** int(data[0])
    exponent = 2 ** (-127 + sum(int(a) * 2 ** b for a, b in zip(data[1:9], range(7, -1, -1))))
    fraction = 1 + sum(int(a) * 2 ** b for a, b in zip(data[9:], range(-1, -24, -1)))
    return sign * exponent * fraction

def float_to_binary(data):
    import struct
    bins = struct.pack('>f', data)
    return ''.join('{:0>8}'.format(bin(i)[2:]) for i in bins)

参考

  1. https://zh.wikipedia.org/wiki/IEEE_754
  2. https://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html
  3. https://zh.wikipedia.org/wiki/%E7%A7%91%E5%AD%A6%E8%AE%B0%E6%95%B0%E6%B3%95
  4. 《深入理解计算机系统》