0%

variable-precision SWAR 算法详解

发表于 更新于 分类于
本文字数： 2.4k 阅读时长 ≈ 3 分钟

在学习redis源码时，发现BITCOUNT命令实现用到了variable-precision SWAR 算法。

BITCOUNT命令要解决的问题：统计一个位数组中非0二进制位的数量。在数学上被称为“计算汉明重量（Hamming Weight)”

目前已知效率最好的通用算法为variable-precision SWAR 算法。
该算法通过一系列位移和位运算操作，可以在常数时间内计算多个字节的汉明重量，并且不需要使用任何额外的内存。

代码

以下是一个处理32位长度位数组的算法实现，一共分4步。

1
2
3
4
5
6
7
uint32_t swar(uint32_t i){
    i = (i & 0x55555555) + ((i>>1) & 0x55555555);  // 步骤1
    i = (i & 0x33333333) + ((i>>2) & 0x33333333);  // 步骤2
    i = (i & 0x0F0F0F0F) + ((i>>4) & 0x0F0F0F0F);  // 步骤3
    i = (i * 0x01010101) >> 24;                    // 步骤4
    return i;
}

解析

这里我们以i=0x12345678(二进制位为00010010001101000101011001111000)为例，讲解算法过程
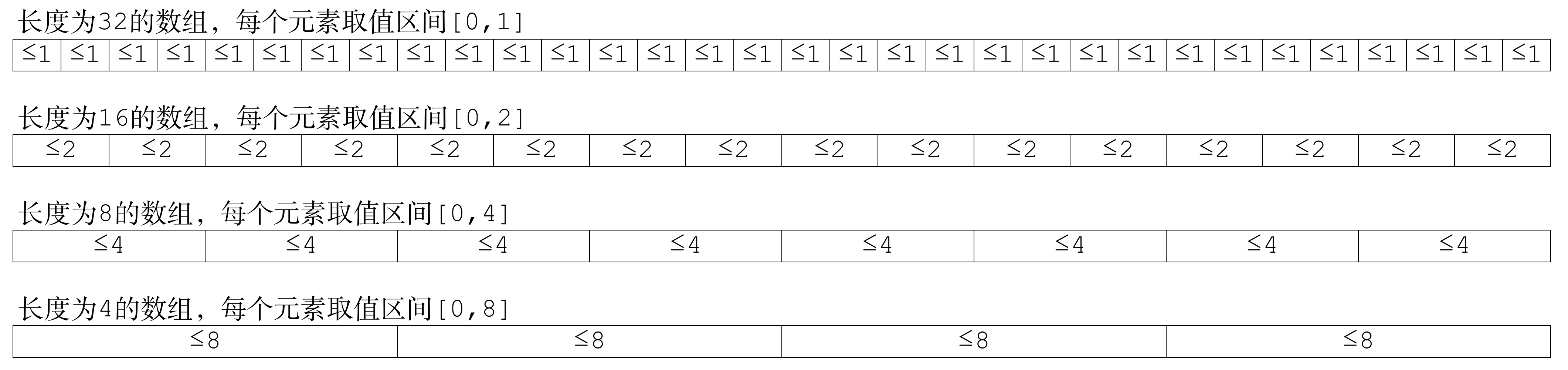
我们可以把i的二进制位理解成：长度为32的数组，每个元素取值区间[0,1]，每个元素正好能代表这个位是不是1.

所以，问题就可以转化为，求这个数组的和。
根据分治法的思想，我们可以把相邻的两个数字相加，得到长度为16的数组，每个元素取值区间[0,2]。
并以此类推，最终求出总和。


步骤1

这一步用到0x55555555作为掩码，其二进制表示为01010101010101010101010101010101
此时i可理解为长度为32的数组，每个元素取值区间[0,1]，元素宽度1bit。

通过i & 0x55555555运算，取得了i的奇数位置元素，存储为16个2bit整数；
通过(i>>1) & 0x55555555运算，取得了i的偶数位置元素，存储为16个2bit整数；

两者相加，相当于16组2bit整数按位相加，问题就转化成了2bit的二进制加法。
由于原数组每个元素取值区间[0,1]，所以每组相加的结果会在[0,2]区间内，2bit刚好存储。
最终得到长度为16的数组，每个元素取值区间[0,2]。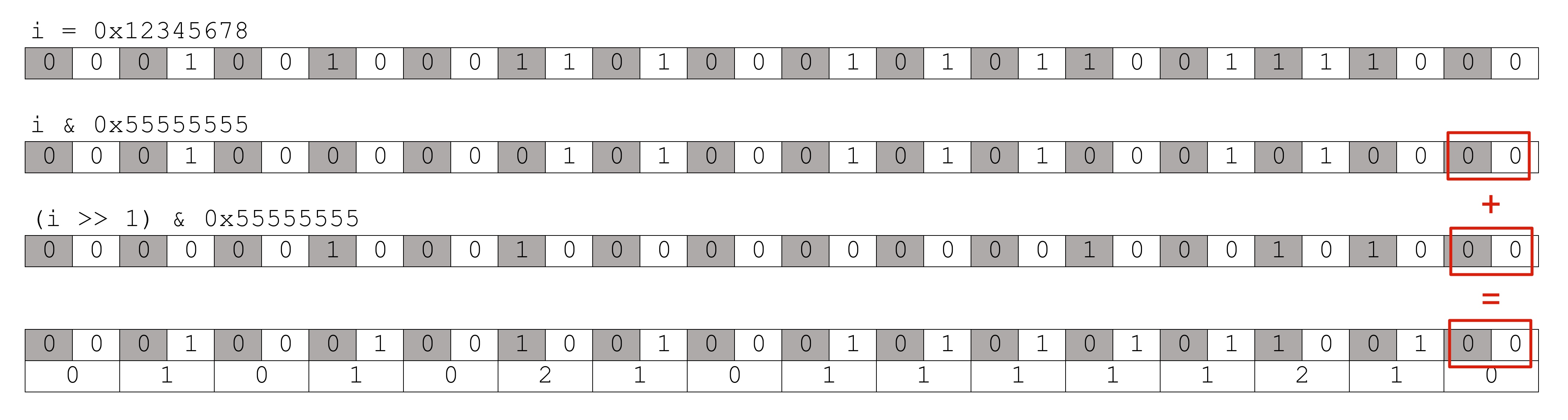

步骤2

这一步用到0x33333333作为掩码，其二进制表示为00110011001100110011001100110011
此时i可理解表示为长度为16的数组，每个元素取值区间[0,2]，元素宽度2bit。

通过i & 0x33333333运算，取得了i的奇数位置元素，存储为8个4bit整数；
通过(i>>1) & 0x33333333运算，取得了i的偶数位置元素，存储为8个4bit整数；

两者相加，相当于8组4bit整数按位相加，问题就转化成了4bit的二进制加法。
由于原数组每个元素取值区间[0,2]，所以每组相加的结果会在[0,4]区间内，4bit刚好存储。
最终得到长度为8的数组，每个元素取值区间[0,4]。

步骤3

这一步用到0x0F0F0F0F作为掩码，其二进制表示为00001111000011110000111100001111
此时i可理解表示为长度为8的数组，每个元素取值区间[0,4]，元素宽度4bit。

通过i & 0x0F0F0F0F运算，取得了i的奇数位置元素，存储为4个8bit整数；
通过(i>>1) & 0x33333333运算，取得了i的偶数位置元素，存储为4个8bit整数；

两者相加，相当于4组8bit整数按位相加, 问题就转化成了8bit的二进制加法。
由于原数组每个元素取值区间[0,4]，所以每组相加的结果会在[0,8]区间内，8bit足够存储。
最终得到长度为4的数组，每个元素取值区间[0,8]。

步骤4

按照上面的思路，本来应该继续将长度为4的数组转换为长度为2的数组。
但是这里由于4个8bit整数相加存在简便运算，就不继续往下合并了。

到这一步是时i=0x02030404，为了求出最终结果，我们可以想到位移的办法将每8bit取出（参考ip掩码计算），然后再依次相加。
最终结果也就是 (i & 0xFF) + ((i>>8) & 0xFF) + ((i>>16) & 0xFF) + ((i>>24) & 0xFF)

为了理解算法里的做法，这里需要简单的数学推导

1
2
3
4
5
6
7
8
9
10
// 将0x01010101转化成多项式表达
          0x01010101 == 2**24 + 2**16 + 2**8 + 2**0
// 两边同乘以i
      i * 0x01010101 == i * 2**24 + i * 2**16 + i * 2**8 + i * 2**0
// 2的乘方运算转化为位移运算
      i * 0x01010101 == (i<<24) + (i<<16) + (i<<8) + (i<<0)
// 两边同时右移24位
(i * 0x01010101)>>24 == ((i<<24)>>24) + ((i<<16)>>24) + ((i<<8)>>24) + ((i<<0)>>24)
// 将左移和右移合并，并考虑溢出，最终结果一致
(i * 0x01010101)>>24 == (i & 0xFF) + ((i>>8) & 0xFF) + ((i>>16) & 0xFF) + ((i>>24) & 0xFF)